Knight's tour puzzle
Introduction
Before I start I would like to make a small announcement. If you are interested in the Julia language you are welcome to participate in a 4-day “Introduction to Julia for Data Science” short course that is organized at MIT on Jan 17-20, 2023. Everyone is invited. You can find a PDF with the schedule here.
Now we can get back to the usual blogging business.
After my recent post about knight covering puzzle I was asked for another puzzle-solving content. Therefore today I want to present you how the Knight’s tour problem can be cracked using Julia.
The code in this post was tested under Julia 1.8.2 and Plots.jl 1.35.0.
The puzzle
Consider a rectangle grid. We place a chess knight in one of the squares on this grid. A chess knight can move two squares vertically and one square horizontally, or two squares horizontally and one square vertically.
We want to find a sequence of moves of a knight so that it visits each square on a grid exactly once and goes back to a starting position.
I will show you how to find a solution to this problem (or learn that the task is impossible) for arbitrary grid sizes. Next, we will see the solution for a standard chessboard that has 8 rows and 8 columns.
The code
In the solution the key object that we will track is a grid. It will
be a matrix storing consecutive moves of a knight. In this matrix a 0
entry means that the square has not visited yet it and positive entry indicates
move number when the square was visited. So number 1 is a starting position of
the knight.
To track location of the knight on a grid we will use a 2-tuple holding
current row and column location of the knight. It is called p in the code.
We first create the listoptions helper function. It takes grid and p
as arguments and returns a vector of possible moves of the knight from p
to squares that have not been visited yet. Here is its implementation:
listoptions(grid, p) =
[p .+ d for d in ((1, 2), (-1, 2), (1, -2), (-1, -2),
(2, 1), (-2, 1), (2, -1), (-2, -1))
if get(grid, p .+ d, -1) == 0]
Notice how nicely the get function works in this case. We use it to get
a -1 value in case p .+ d is not within bounds of grid (so such invalid
moves are discarded).
It is time to present a key function that will handle the traversal of the
grid by the knight:
function knight_jump!(grid=fill(0, 8, 8), p=(1, 1), i=1)
grid[p...] = i
if i == length(grid)
p1 = Tuple(findfirst(==(1), grid))
return extrema(abs, p .- p1) == (1, 2) ? grid : nothing
end
v = listoptions(grid, p)
sort!(v, by=np -> length(listoptions(grid, np)))
for np in v
knight_jump!(grid, np, i + 1) !== nothing && return grid
end
grid[p...] = 0
return nothing
end
Let me explain how it works. The grid and p arguments were already
discussed. The extra i argument stores the move number. The function
returns grid in case it found a feasible solution and nothing if no
feasible solution is found. This invariant is crucial, as we will use it
to perform depth first search for a valid knight tour.
First we set the grid at location p to i to record the current placement
of the knight.
Next in i == length(grid) check we verify that we have hit the last free spot
on a grid. If this is the case we check if the current position p is
knight-jump away from the initial position of the knight (denoted by p1 in
the code). If this is the case we return grid. Otherwise the tour is invalid
and we return nothing.
If our tour is not finished yet we store in the v vector the possible moves
we can do next. Now a crucial part of the algorithm is applied. We sort v
using Warnsdorff’s rule, that is, we put the squares with fewest
onward moves in the front of the verctor. We then recursively visit them
and try to solve the puzzle. If we succeed, i.e. when the recursive call
to knight_jump! does not return nothing, we are done and return the result.
If we fail for all values in v, this means that an attempt to visit p was
an incorrect choice. In this case we need to reset grid so that in position
p it has 0 and return nothing (to signal a problem).
The result
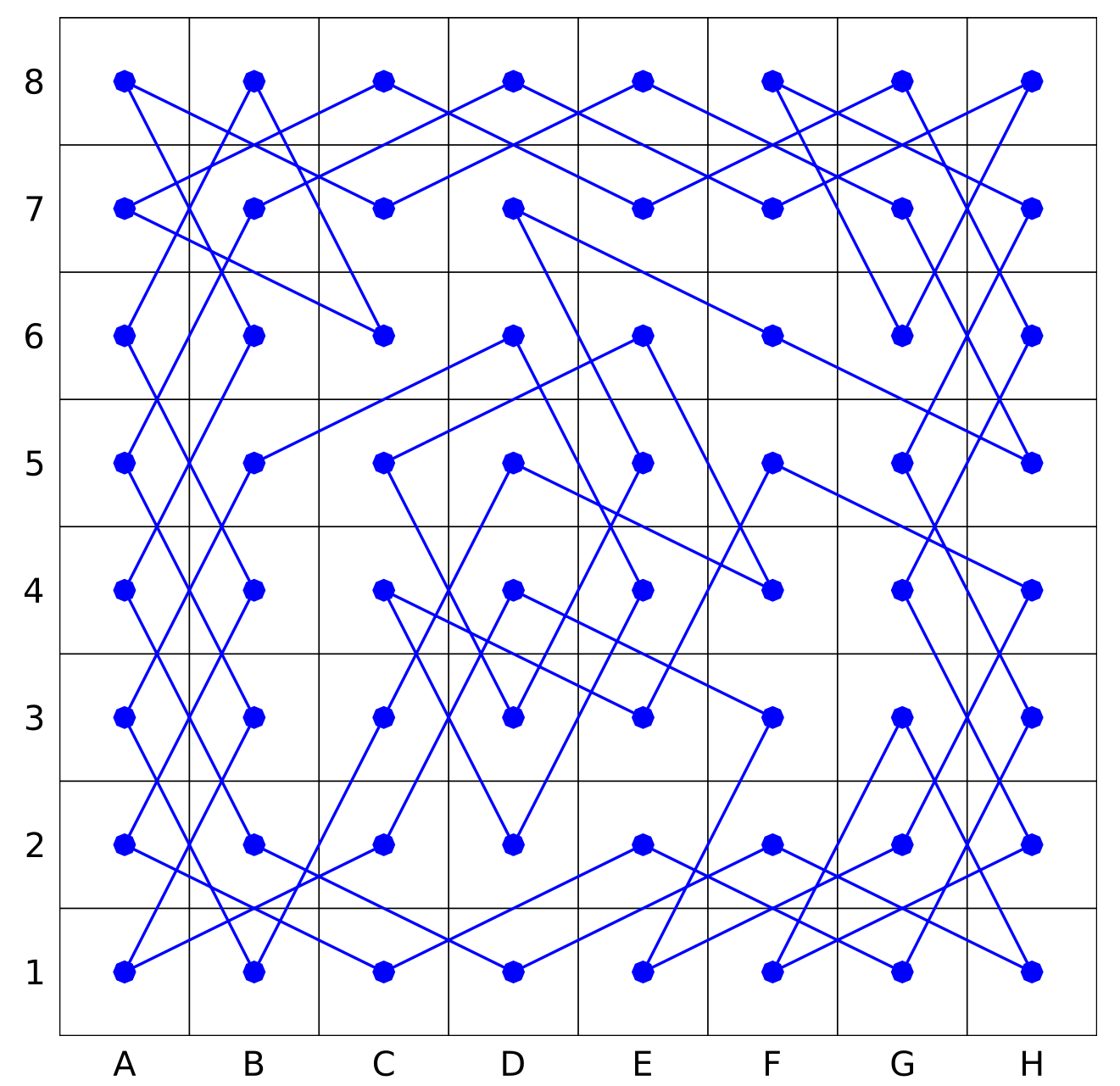
Let us check how the solution looks on a 8x8 grid (which is the default in our code):
julia> res = knight_jump!()
8×8 Matrix{Int64}:
1 16 51 34 3 18 21 36
50 33 2 17 52 35 4 19
15 64 49 56 45 20 37 22
32 55 44 63 48 53 42 5
61 14 57 54 43 46 23 38
28 31 62 47 58 41 6 9
13 60 29 26 11 8 39 24
30 27 12 59 40 25 10 7
First we see that indeed the solution was found (as we did not get nothing
from the call). Second, a visual inspection of the solution shows that indeed
the solution is correct.
Let us additionally visualize it to make the analysis easier. We first convert
the res matrix into the moves vector of consecutive knight locations stored
as tuples. Next we add first location to the end of this vector (as we have
a cycle). Finally we plot a chessboard with consecutive knight moves presented
by lines.
julia> using Plots
julia> moves = Tuple.(CartesianIndices(res)[sortperm(vec(res))])
64-element Vector{Tuple{Int64, Int64}}:
(1, 1)
(2, 3)
(1, 5)
⋮
(6, 3)
(4, 4)
(3, 2)
julia> push!(moves, first(moves))
65-element Vector{Tuple{Int64, Int64}}:
(1, 1)
(2, 3)
(1, 5)
⋮
(4, 4)
(3, 2)
(1, 1)
julia> plot(getindex.(moves, 1), getindex.(moves, 2);
legend=false, size=(400, 400), color=:blue,
marker=:o, markerstrokecolor=:blue,
xlim=(0.5, 8.5), ylim=(0.5, 8.5),
minorticks=2, minorgrid=true, grid=false,
xticks=(0:9, [""; 'A':'H'; ""]), yticks=0:9,
minorgridalpha=1.0, showaxis=false)
The resulting plot looks as follows:
Homework
Since I have started the post with an announcement of a short course, let me switch to lecturing mode for a moment. For this puzzle I have the following exercises for you to train your Julia muscle:
- Check if we ever need to backtrack in the algorithm as maybe we solve the problem on the first attempt thanks to Warnsdorff’s rule?
- Measure the performance of the code.
- Do you have ideas how its speed could be improved (hint: think how you can reduce the number of allocations and avoid sorting)
- Check what would happen if we did not use Warnsdorff’s rule. Two natural
candidate rules are: visiting squares in random order and visiting squares in
the order produced by the
listoptionsfunction. - The proposed solution uses recursion. Since Julia has a recursion depth limit the code will not work as expected for large grids. First, find this limit. Second, think how you could rewrite the program so that it avoids using recursion.
Conclusions
I hope you enjoyed the puzzle and the presented solution. If you get stuck on any parts of the homework we can discuss them in January, 2023 at MIT during the short course or just contact me on Julia Discourse or Julia Slack and I will gladly answer your questions.