Summer break puzzle

Introduction

After an amazing JuliaCon 2021 this week I thought to cover some lightweight topic in my post.

An interesting question I recently was asked is to find \(x\in\mathbf{R}^+\cup\{0\}\) that maximizes \(x^{1/x}\) (assuming that in \(0\) the value of the function is established by the limit as \(x\to0^+\)).

As usual I will want to use Julia to get some insight into this problem before giving it a try.

This post was tested under Julia 1.6.1, Plots.jl 1.20.0, Optim.jl 1.4.1, and Symbolics.jl 2.0.

Plotting

We start with plotting of the function we want to investigate:

julia> using Plots

julia> plot(x -> x^(1/x), 0, 10, legend=nothing,
            xlab=raw"$x$", ylab=raw"$x^{1/x}$")

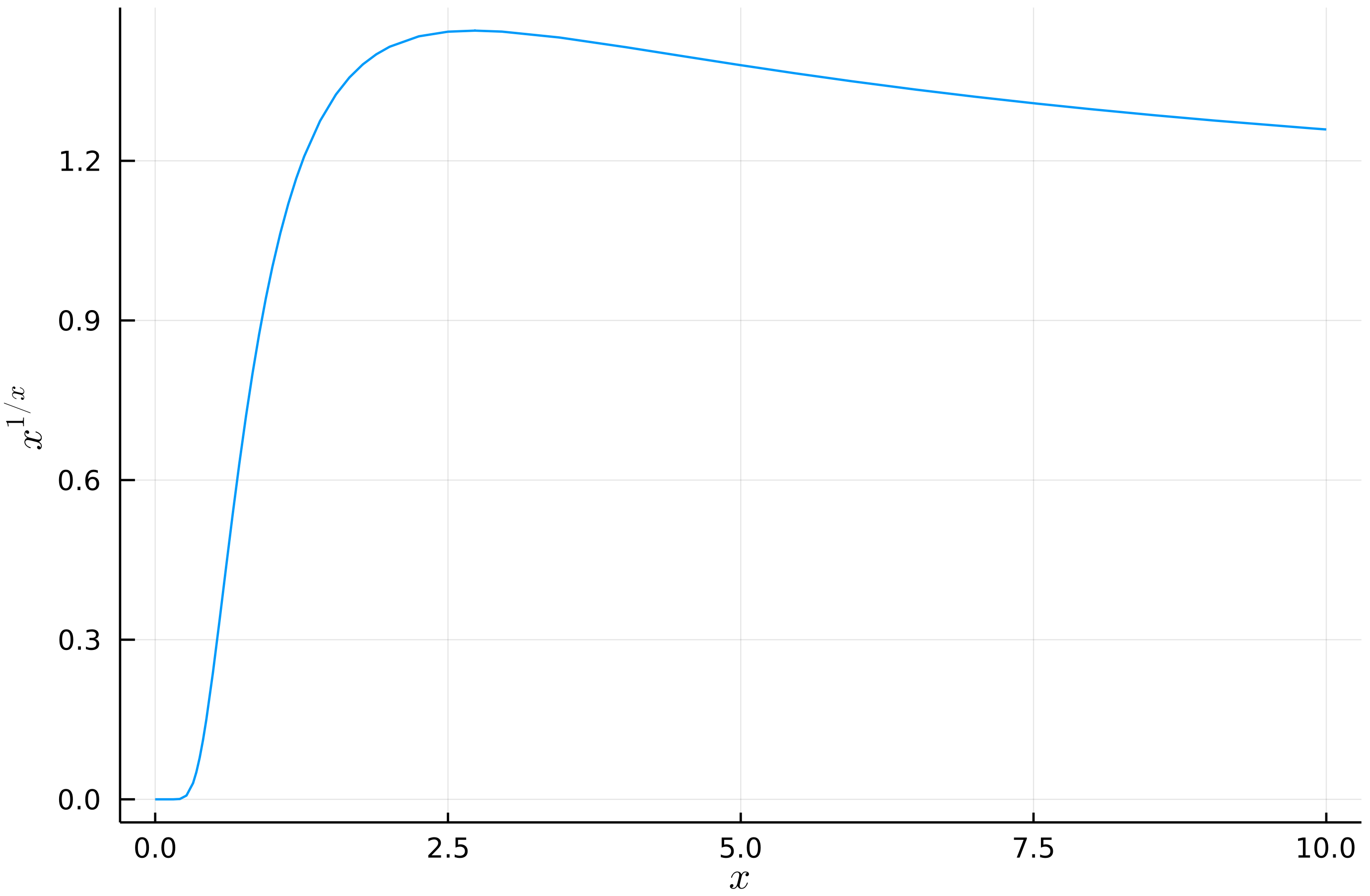
It seems that the maximum is achieved around \(2.5\), but we want to get more a detailed answer.

Optimizing

Now we switch to optimization to find the value that maximizes our function numerically. Note that I optimize x -> -x^(1/x) (negated), as optim by default is looking for a minimum of a function.

julia> using Optim

julia> optimize(x -> -x^(1/x), 0, 10)
Results of Optimization Algorithm
 * Algorithm: Brent's Method
 * Search Interval: [0.000000, 10.000000]
 * Minimizer: 2.718282e+00
 * Minimum: -1.444668e+00
 * Iterations: 13
 * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true
 * Objective Function Calls: 14

The optimal solution looks to be equal to \(e\). Let us verify this using calculus.

Solving

Now we check if the derivative of our function is equal to zero for \(e\) as an argument.

julia> using Symbolics

julia> @variables x
1-element Vector{Num}:
 x

julia> ex = Differential(x)(x^(1/x)) |> expand_derivatives |> simplify
x^(x^-1 - 2) - (log(x)*(x^(x^-1 - 2)))

julia> substitute(ex, x => MathConstants.e)
0.0

From the form of ex we also see that \(e\) is the only zero of our derivative for positive values of \(x\).

Now I am convinced enough about the result to try proving it using some elementary arguments.

Pen and paper

Note that:

\[x^{1/x} = e^{\log(x)/x}\]

As exponential function is increasing it is enough to analyze \(\log(x)/x\), which hopefully will be simpler. Substitute \(x = e^y\), where \(x\to0^+\) as \(y\to-\infty\). With this substitution we get that we need to analyze:

\[\frac{y}{e^y}.\]

Now notice that as \(y\to-\infty\) the fraction tends to \(-\infty\), so our original expression \(x^{1/x}\) tends to \(0^+\) as \(x\to0^+\). Similarly if \(y\to+\infty\) the fraction tends to \(0^+\), so \(x^{1/x}\) tends to \(1\) as \(x\to+\infty\).

Having done this warm up task let us ask what \(y\) maximizes \(y/e^y\). From our earlier analyses we postulate that it is maximized for \(y=1\), so we want to show that:

\[\frac{y}{e^y} \leq \frac{1}{e}\]

or, equivalently, substituting \(z=y-1\):

\[1+z \leq e^z.\]

This is a well known consequence of Bernoulli’s inequality and the equality holds for \(z=0\), which translates to \(x=e\).

Conclusions

I hope you enjoyed the post. Next week I will be back with DataFrames.jl related topics, so stay tuned.